dev-notes/docs/databases/database-systems/b+trees.md

Indexes & B+Trees

B+Tree

B+Tree Visualization

A B+Tree is a self-balancing tree data structure that keeps data sorted and allows searches, sequential access, insertions and deletions always in O(log n).
It's a generalization of a binary search tree, since a node can have more than two children. It's optimized for systems that need to read and write large blocks of data.

A B+Tree is an M-way search tree with the following properties:

• It's perfectly balanced (every leaf node is at the same depth).
• Every node other than the root is at least half-full ((M/2)-1 <= #keys <= M-1).
• Every inner node with k keys has k+1 non-null children.

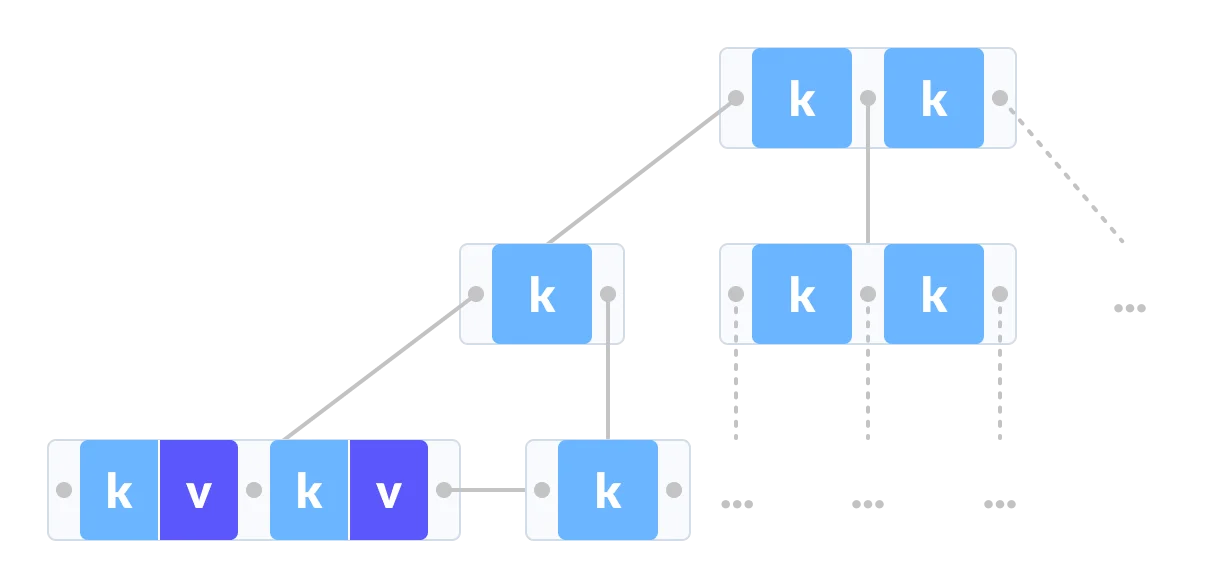
Nodes

Every B+Tree node is comprised if an array of key-value pairs. The keys are derived from the attribute(s) that the index is based on. The values will differ based on whether the node is classified as an inner node or a leaf node.

The arrays are (usually) kept in sorted key order.

Leaf node values:

• Record ID: pointer to the location of the tuple to which the index entry corresponds.
• Tuple Data: the leaf node stores the actual contents of the tuple. Secondary indexes must store the record id a their values.

Note

: if the workload is mostly primary key lookup then prefer index with tuple data. If the workload has several secondary key lookups prefer record ids. Tuple data indexes need a double search for secondary keys since a secondary index will return a primary key to be searched again in the primary index.

B-Tree bs B+Tree

The B-Tree stores keys and values in all nodes of the tree. It's more space-efficient since each key only appears once in the tree.

A B+Tree only stores values in leaf nodes, inner nodes only guide the search process. Since the values are in a linked list at the bottom of the tree a sequential scan does not need to jump around the tree.

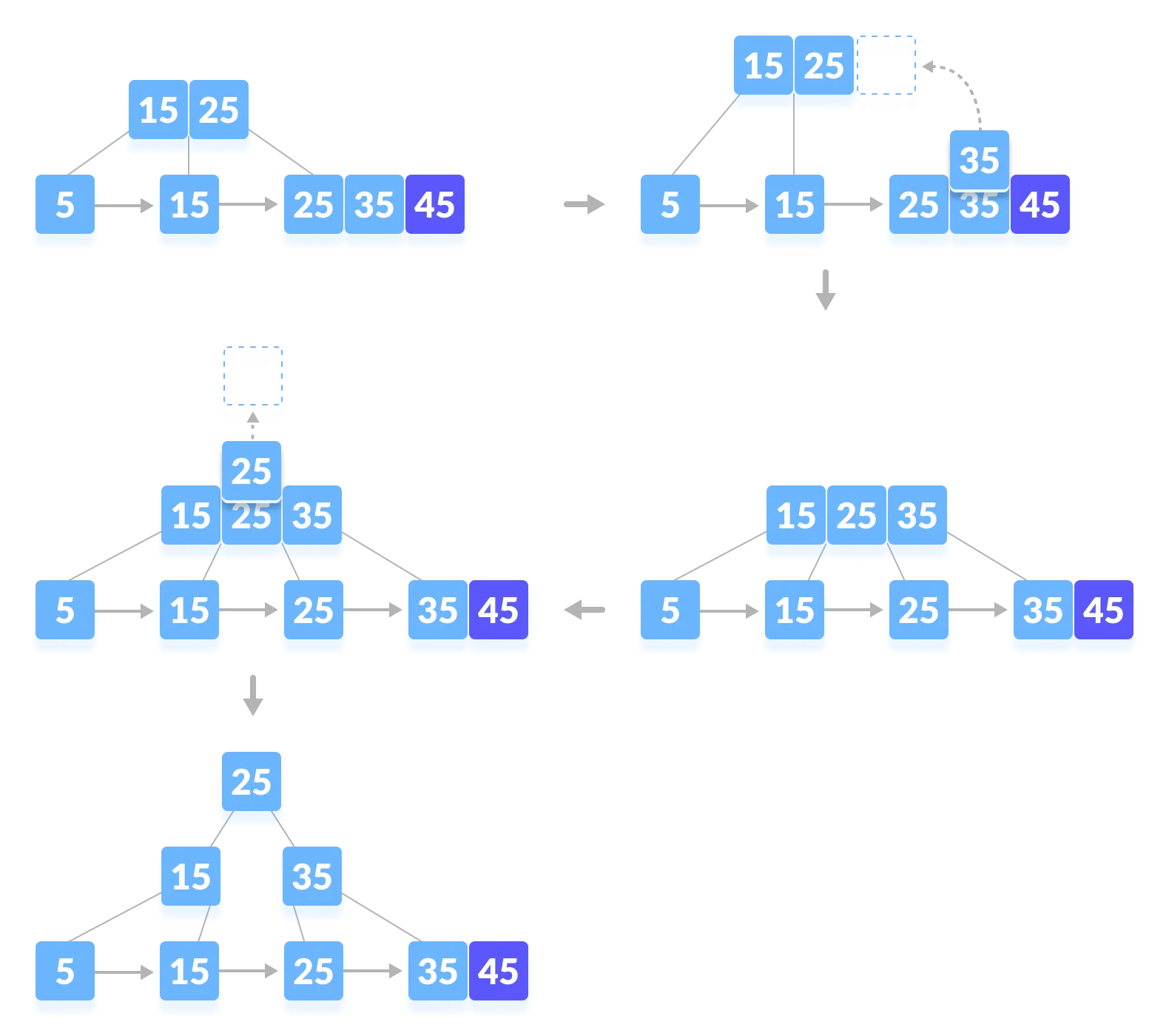
Insertion

Find leaf node in which the entry belongs.

• Case 1: If the leaf is not full, insert the key into the leaf node in increasing order. Done.
• Case 2: If the leaf is full, insert the key into the leaf node in increasing order and balance the tree:
  1. Break the node at M/2th position. New leaf contains M/2..M-1 nodes.
  2. Add M/2th key to the parent node as well.
  3. If the parent node is already full, follow steps 2 to 3.

Note

B+Trees grow at the root and not at the leaves.

Deletion

Find leaf node in which the entry belongs and remove the entry.

• Case 1: The leaf has more than M/2 entries. Done.
• Case 2: The leaf has only (M/2)-1 entries. Two options:
  • re-distribute borrowing from sibling, update parent if needed.
  • merge with sibling, must delete entry from parent.

Note

: merging can bubble up and reduce the depth of the tree.

Key Lookups

A DBMS can use a B+Tree index if the query provides any of the attributes of the search key. For an hash index all attributes of the key are needed.

Note

: not all DBMSs support partial key lookup if the leading attribute is missing

Duplicate Keys

• Append Record Id: Add the tuple's unique record id as part of the key to ensure all keys are unique. The DBMS can still use partial keys to find tuples.
• Overflow Leaf Nodes: Allow leaf nodes to split into overflow nodes that contain the duplicate keys (more complex to maintain and modify).